Publications
2026
- ICLR
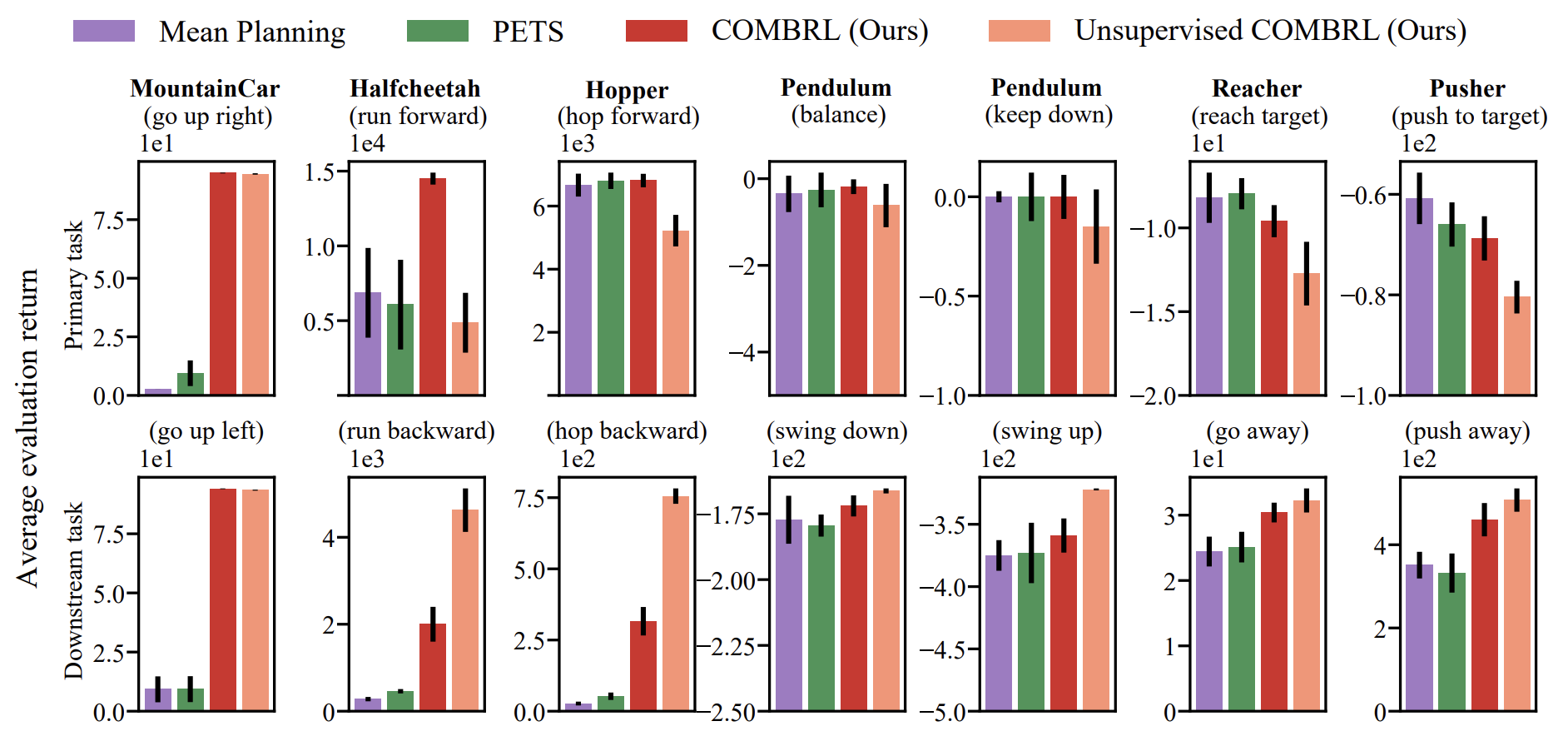 Sample-efficient and Scalable Exploration in Continuous-Time RLarXiv preprint arXiv:2510.24482, 2026
Sample-efficient and Scalable Exploration in Continuous-Time RLarXiv preprint arXiv:2510.24482, 2026 - ICRA
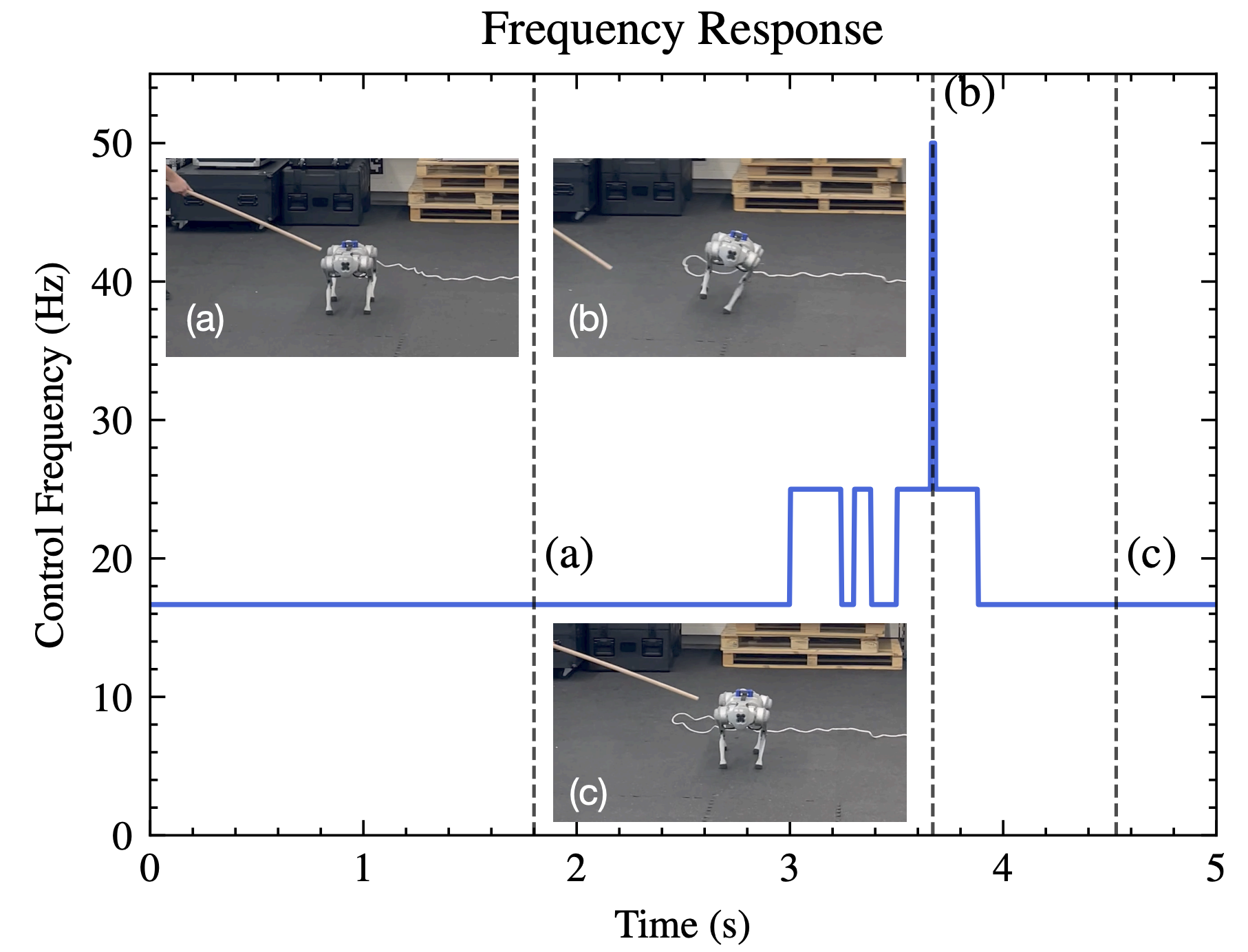
2025
- Under review
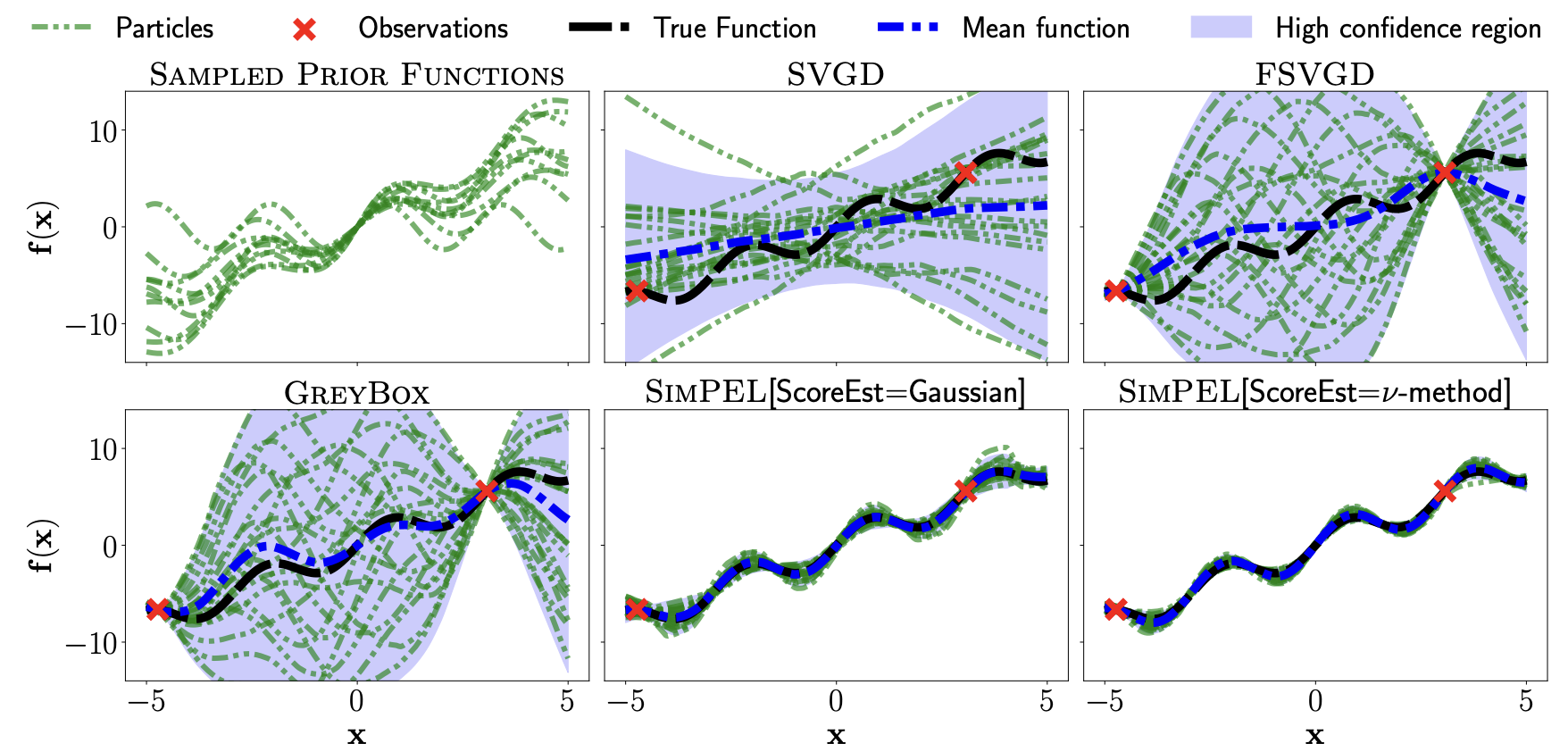
- NeurIPS
 Optimism via intrinsic rewards: Scalable and principled exploration for model-based reinforcement learningAdvances in Neural Information Processing Systems, 2025
Optimism via intrinsic rewards: Scalable and principled exploration for model-based reinforcement learningAdvances in Neural Information Processing Systems, 2025 - ICLR
 ActSafe: Active Exploration with Safety Constraints for Reinforcement LearningIn The Thirteenth International Conference on Learning Representations, 2025
ActSafe: Active Exploration with Safety Constraints for Reinforcement LearningIn The Thirteenth International Conference on Learning Representations, 2025
2024
- NeurIPS
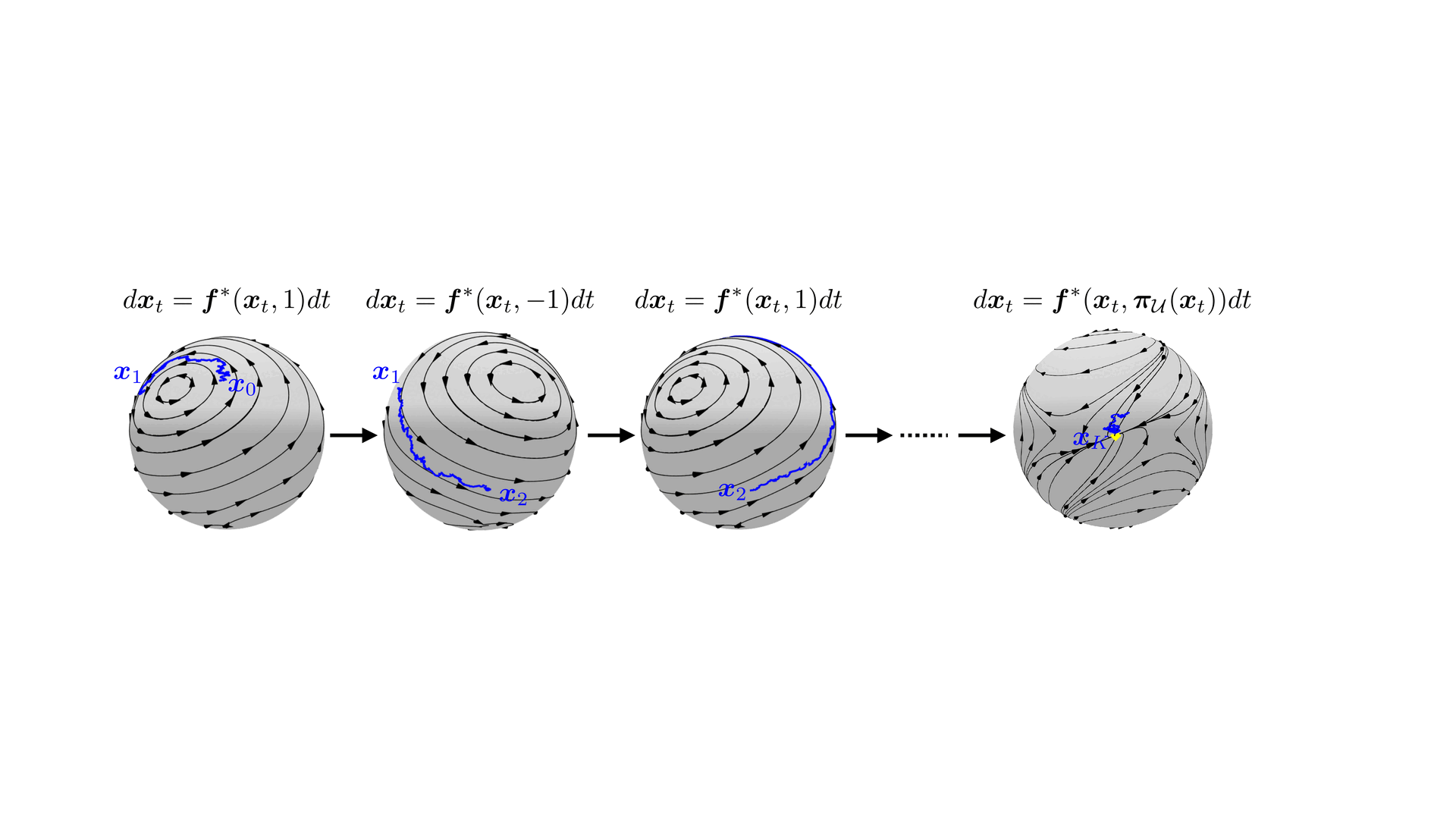 When to sense and control? a time-adaptive approach for continuous-time RLAdvances in Neural Information Processing Systems, 2024
When to sense and control? a time-adaptive approach for continuous-time RLAdvances in Neural Information Processing Systems, 2024 - NeurIPS
 Neorl: Efficient exploration for nonepisodic rlAdvances in Neural Information Processing Systems, 2024
Neorl: Efficient exploration for nonepisodic rlAdvances in Neural Information Processing Systems, 2024 - NeurIPS
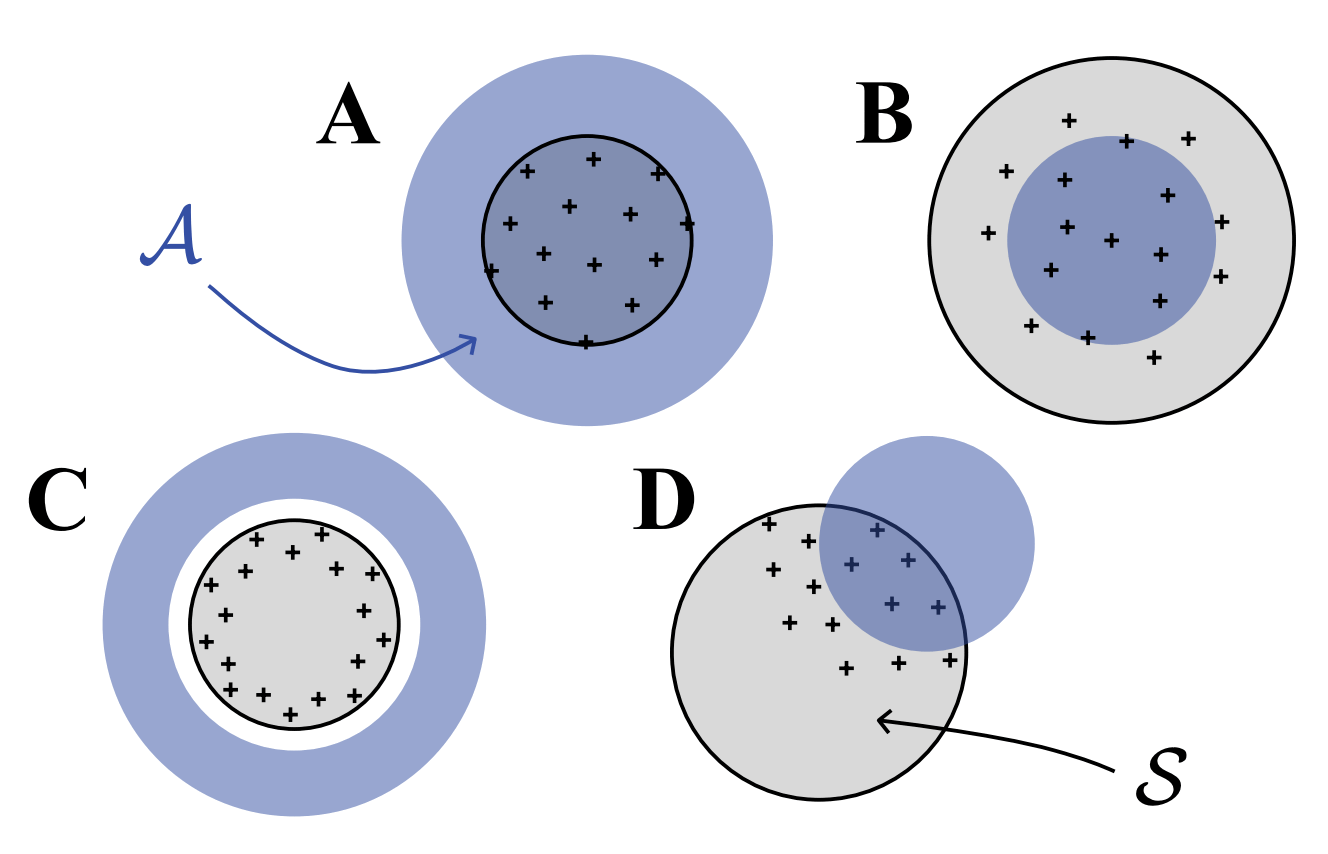 Transductive active learning: Theory and applicationsAdvances in Neural Information Processing Systems, 2024
Transductive active learning: Theory and applicationsAdvances in Neural Information Processing Systems, 2024 - IROS
 Bridging the sim-to-real gap with Bayesian inferenceIn 2024 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), 2024
Bridging the sim-to-real gap with Bayesian inferenceIn 2024 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), 2024 - ICLR Workshop
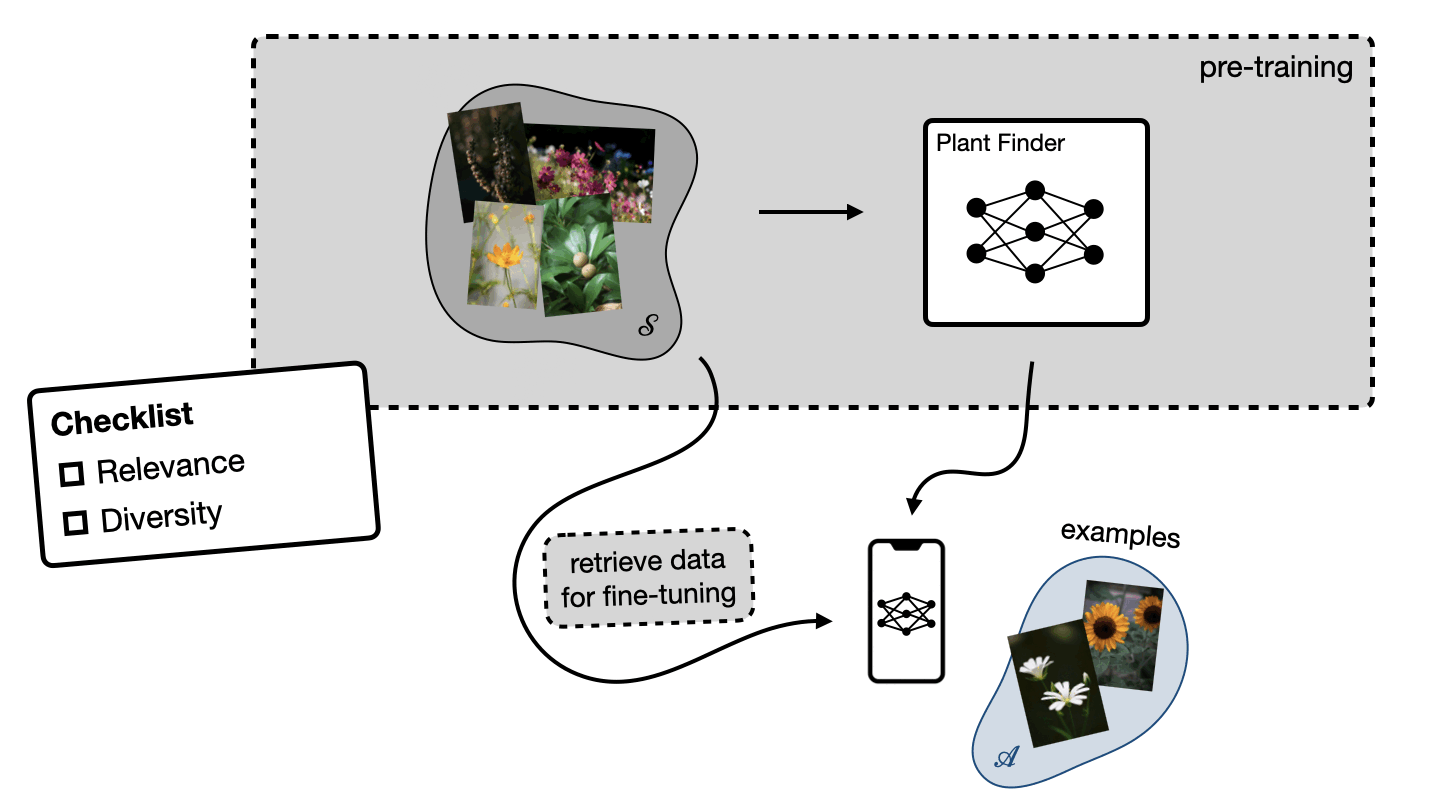
2023
- NeurIPS
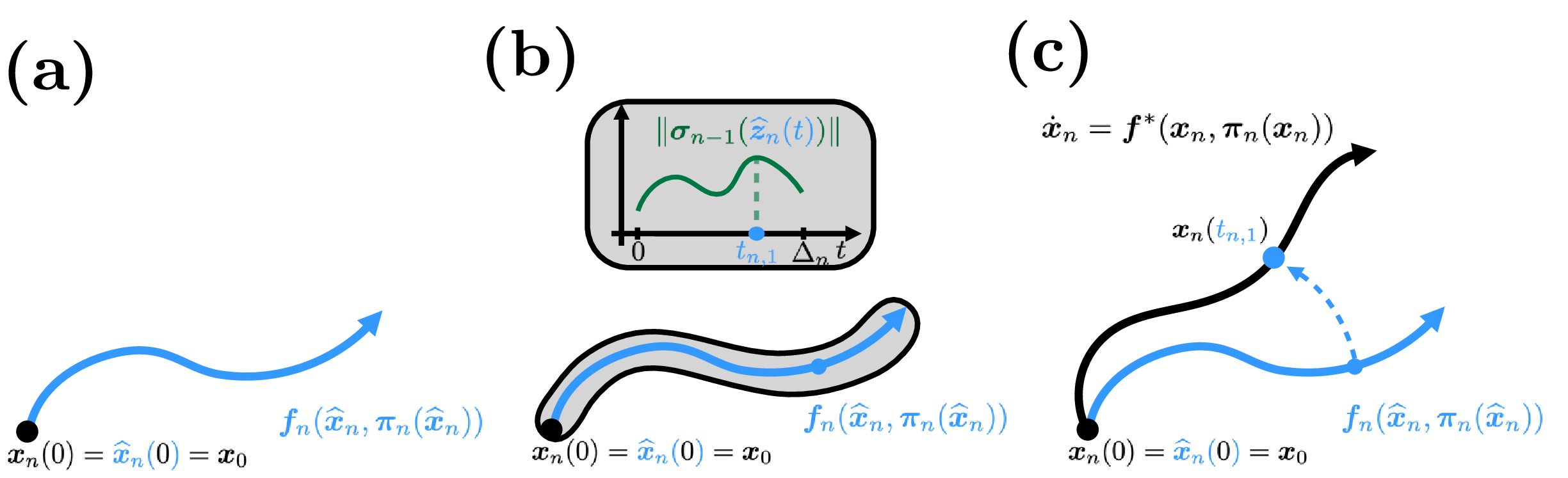 Efficient exploration in continuous-time model-based reinforcement learningAdvances in Neural Information Processing Systems, 2023
Efficient exploration in continuous-time model-based reinforcement learningAdvances in Neural Information Processing Systems, 2023 - NeurIPS
 Optimistic active exploration of dynamical systemsAdvances in Neural Information Processing Systems, 2023
Optimistic active exploration of dynamical systemsAdvances in Neural Information Processing Systems, 2023
2021
- NeurIPS
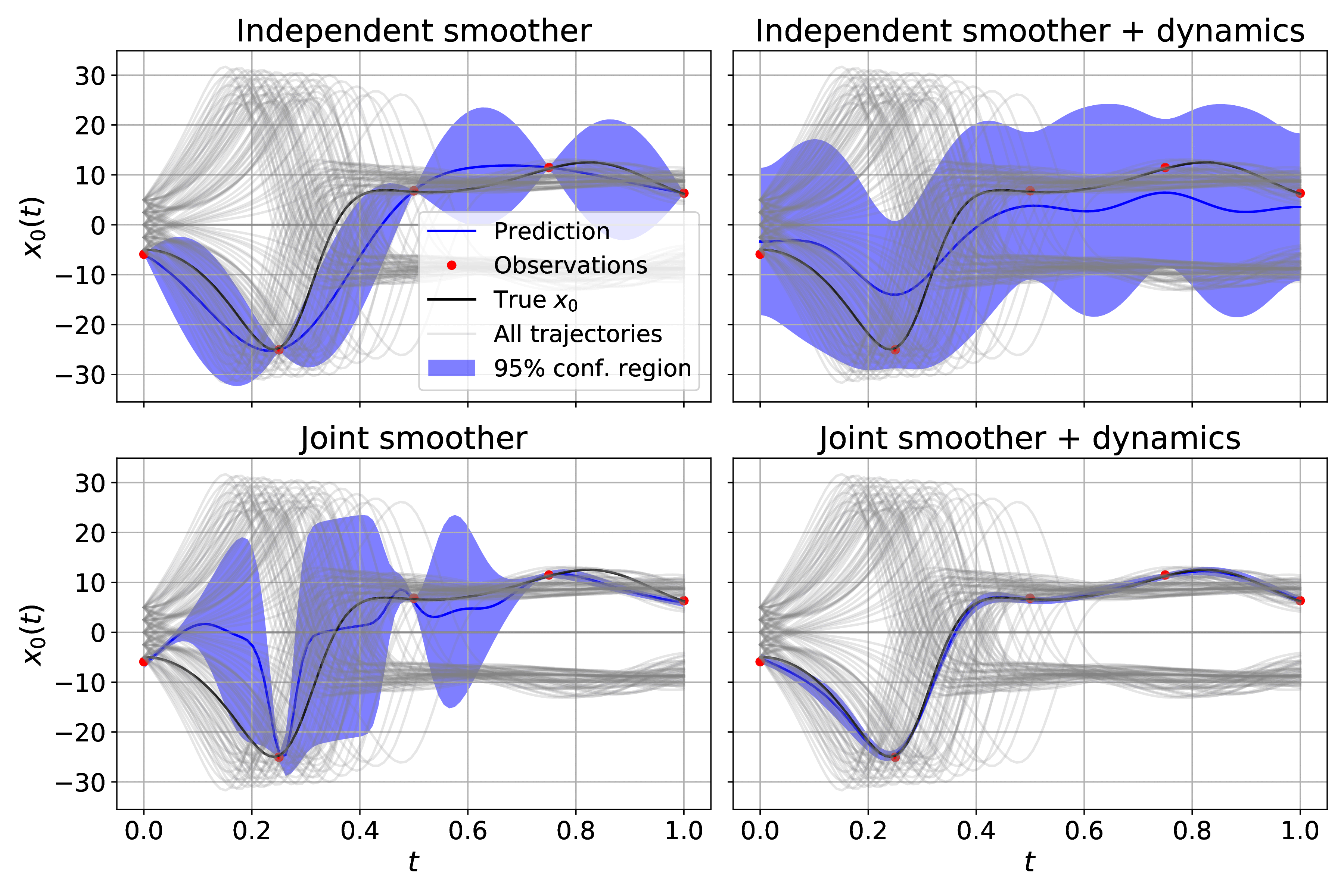 Distributional gradient matching for learning uncertain neural dynamics modelsAdvances in Neural Information Processing Systems, 2021
Distributional gradient matching for learning uncertain neural dynamics modelsAdvances in Neural Information Processing Systems, 2021 - L4DC
 Learning stabilizing controllers for unstable linear quadratic regulators from a single trajectoryIn Learning for dynamics and control, 2021
Learning stabilizing controllers for unstable linear quadratic regulators from a single trajectoryIn Learning for dynamics and control, 2021